快捷导航
上海总部：上海市普陀区宁夏路201号绿地科创大厦6楼D座
邮编：200063
总机：021-31358878、52363421
传真：021-31358878-8010
业务邮箱：
guandq@hmelectronics.com.c
n
邮编：200063
总机：021-31358878、52363421
传真：021-31358878-8010
业务邮箱：
guandq@hmelectronics.com.c
n
资讯文章
正弦电路的无功功率和功率因数
正弦电路的无功功率和功率因数
在正弦电路中，负载是线性的，电路中的电压和电流都是正弦波。设电压和电流可分别表示为
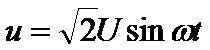
正弦电路的无功功率和功率因数-图1
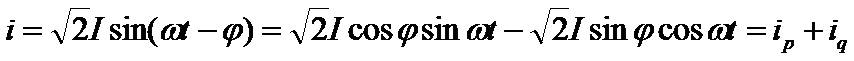（2-22）正弦电路的无功功率和功率因数-图2
式中 φ——电流滞后电压的相角。
电流 被分解为和电压同相位的分量ip和比电压滞后90°的分量iq。ip和iq分别为
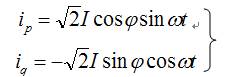（2-23）正弦电路的无功功率和功率因数-图3
电路的有功功率P就是其平均功率，即
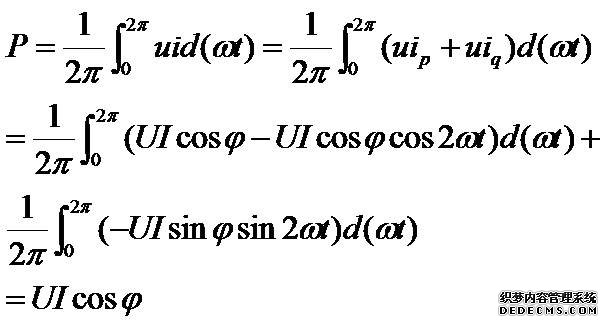(2-24)正弦电路的无功功率和功率因数-图4
电路的无功功率定义为
（2-25）正弦电路的无功功率和功率因数-图5
可以看出，Q就是式（2-24）中被积函数的第2项无功功率分量uiq的变化幅度。uiq的平均值为零，表示了其有能量交换而并不消耗功率。Q表示了这种能量交换的幅度。在单相电路中，这种能量交换通常是在电源和具有储能元件的负载之间进行的。从式（2-24）可看出，真正的功率消耗是由被积函数的第1项有功功率分量uip产生的。因此，把由式（2-23）所描述的ip和iq分别称为正弦电路的有功电流分量和无功电流分量。
对于发电机和变压器等电气设备来说，其额定电流值与导线的截面积及铜损耗有关，其额定电压和绕组电气绝缘有关，在工作频率一定的情况下，其额定电压还和铁心尺寸及铁心损耗有关。因此，工程上把电压电流有效值的乘积作为电气设备功率设计极限值，这个值也就是电气设备最大可利用容量。因此，引入如下视在功率的概念：
（2-26）正弦电路的无功功率和功率因数-图6
从式（2-24）可知，有功功率P的最大值为视在功率S，P越接近S，电气设备的容量越得到充分利用。为了反映P接近S的程度，定义有功功率和视在功率的比值为功率因数 。
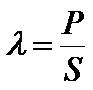(2-27)正弦电路的无功功率和功率因数-图7
从式（2-24）和式（2-26）可以看出，在正弦电路中，功率因数是由电压和电流之间的相角差决定的。在这种情况下，功率因数常用cosφ来表示。
从式（2-24）、式（2-25）和式（2-26）可知，S、P和Q有如下关系：
从式（2-24）、式（2-25）和式（2-26）可知，S、P和Q有如下关系：
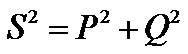(2-28)正弦电路的无功功率和功率因数-图8
应该指出，视在功率只是电压和电流有效值的乘积，它并不能准确反映能量交换和消耗的强度。在一般电路中，视在功率并不遵守能量守恒定律。
主营产品：有源电力滤波器IGBT应用方案,有源滤波器方案定制,apf方案定制,有源滤波器解决方案,apf stack,电力电子积木,感应加热IGBT方案