快捷导航
上海总部：上海市普陀区宁夏路201号绿地科创大厦6楼D座
邮编：200063
总机：021-31358878、52363421
传真：021-31358878-8010
业务邮箱：
guandq@hmelectronics.com.c
n
邮编：200063
总机：021-31358878、52363421
传真：021-31358878-8010
业务邮箱：
guandq@hmelectronics.com.c
n
资讯文章
无功功率的时域分析和三相电路的功率因数
无功功率的时域分析和三相电路的功率因数
上述定义和分析都是建立在傅里叶级数基础上的，属于频域分析。还有一种在时域对无功电流和无功功率进行定义的方法。这种方法是把电流按照电压波形分解成有功电流ip(t)和无功电流iq(t)两个分量，其中ip(t)的波形与电压u(t)完全一致，即
（2-38）无功功率的时域分析和三相电路的功率因数-图1
式中，G为一比例常数，其取值应使一周期ip(t)内所消耗的平均功率和i(t)消耗的平均功率相等，即
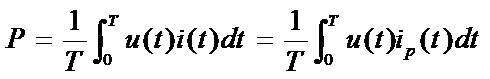（2-39）无功功率的时域分析和三相电路的功率因数-图2
把式（2-38）代入上式可得
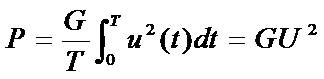
无功功率的时域分析和三相电路的功率因数-图3
由此可求得
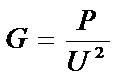（2-40）无功功率的时域分析和三相电路的功率因数-图4
即
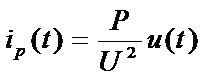（2-41）无功功率的时域分析和三相电路的功率因数-图5
定义无功电流iq(t)为
（2-42）无功功率的时域分析和三相电路的功率因数-图6
由式（2-39）、式（2-41）和式（2-42）可得
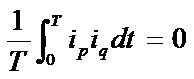（2-43）无功功率的时域分析和三相电路的功率因数-图7
即ip和iq正交。因此可求得i、ip和iq的有效值之间关系如下：
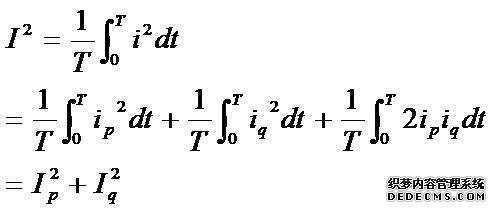
无功功率的时域分析和三相电路的功率因数-图7
考虑到S2=UI,并定义P=UIp、Q=UIq，给上式两边同乘以U2可得
（2-44）无功功率的时域分析和三相电路的功率因数-图8
可以看出，上式和在频域分析法中得出的结论是完全一致的。时域分析的方法是S.Fryze在1932年就提出的[40]，随着电网谐波问题日益严重和现代技术的进步，近年这一定义才又重新引起人们的兴趣。
三相电路的功率因数
在三相对称电路中，各相电压、电流均为对称，功率因数也相同。三相电路总的功率因数就等于各相的功率因数。在三相电路中，影响功率因数的因素除电流和电压的相位差、波形畸变外，还有一个因素就是三相不对称。三相不对称电路的功率因数至今没有统一的定义。定义之一为
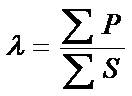(2-45)无功功率的时域分析和三相电路的功率因数-图10
式中，各相的S为其电流与各流到人为中点电压的乘积。可以看出，即使三相都是电阻负载，只要三相不对称，功率因数仍小于1。该定义简单明易于计算，考虑了不对称的因素，但其一举不充分。
另一定义称为矢量功率因数[3]：
另一定义称为矢量功率因数[3]：
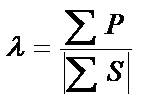（2-46）无功功率的时域分析和三相电路的功率因数-图11
式中，S为矢量，各相S的相角为该相电流滞后电压的角度。
主营产品：有源电力滤波器IGBT应用方案,有源滤波器方案定制,apf方案定制,有源滤波器解决方案,apf stack,电力电子积木,感应加热IGBT方案