无功功率理论的研究及其进展

无功功率理论的研究及其进展

    传统的功率定义大都是建立在平均值基础上的。单相正弦电路或三相对称正弦电路中，利用传统概念定义的有功功率、无功功率、视在功率和功率因数等概念都很清楚。但当电压或电流中含有谐波时，或三相电路不平衡时，功率现象比较复杂，传统概念无法正确地对其进行解释和描述。建立能包含畸变和不平衡现象的完善的功率理论，是电路理论中一个重要的基础性课题。

    学术界有关功率理论的争论可以追溯到20世纪20和30年代，Budeanu和Fryze最早分别提出了在频域定义和在时域定义的方法[39、40]，以后又有各种定义和理论不断出现[41~44]。20世纪80年代以来，新的定义和理论更是不断推出[45~61]。自1991年以来，已多次举办了专门讨论非正弦情况下功率定义和测量问题的国际会议[62、63]，但迄今为止，尚未找到彻底解决问题的理论和方法。新的理论往往是解决了前人未解决好的问题，同时却又存在另一些不足，或引出了新的待解决的问题。对新提出的功率定义和理论应有如下要求[64]：
（1）物理意义明确，能清楚地解释各种功率现象，并能在某种程度上与传统功率理论保持一致；
（2）有利于对谐波源和无功功率的辨识和分析，有利于对谐波和无功功率流动的理解；
（3）有利于对谐波和无功功率的补偿和抑制，能为其提供理论指导；
（4）能够被精确测量，有利于有关谐波和无功功率的监测、管理和收费。

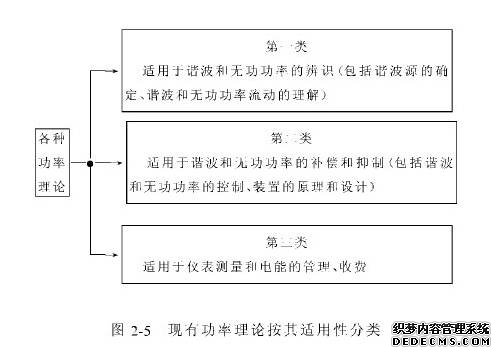
    根据上述要求，可将现有的功率理论分为图2-5所示的三大类。迄今为止的各种功率定义和理论只是较好地解决了上述一两个方面的问题，而未能满足所有要求。Czarnecki和Depenbrock的工作对第一类功率理论问题的解决起了较大的促进作用[45~61]。H.Akagi（赤木泰文）等人提出的瞬时无功功率理论解决了谐波和无功功率的瞬时检测和不用储能元件实现谐波和无功补偿等问题，对谐波和无功补偿装置的研究和开发起到了很大的推动作用。本书将在第6章对这一理论进行专门介绍。但这一理论的物理意义较为模糊，与传统理论的关系不够明确，在解决第一类和第三类问题时遇到困难。对于第三类理论问题的研究虽然取得了一定成果[65~69]，但至今未取得较大突破。总之，如何建立更为完善的功率定义和理论，特别是能为供电企业和电力用户广泛接受，还需进行更多的努力。

无功功率理论的研究及其进展