快捷导航
上海总部:上海市普陀区宁夏路201号绿地科创大厦6楼D座
邮编:200063
总机:021-31358878、52363421
传真:021-31358878-8010
业务邮箱:
guandq@hmelectronics.com.c
n
邮编:200063
总机:021-31358878、52363421
传真:021-31358878-8010
业务邮箱:
guandq@hmelectronics.com.c
n
资讯文章
计及换相过程中的位移因数
计及换相过程中的位移因数
应该说明的是,Dobinson法是忽略换相过程的。但上述求电流纹波比的过程却涉及到了换相重叠角γ和交流电抗LB。为了与Dobinson法原理保持一致,可在计算中令γ和LB均为零。
此外,以上讨论的是交流侧的谐波问题。至于位移因数,则由图3-21波形明显可以看出,由于对换相过程的忽略以及电流波形的对称性,位移因数仍为cosα。
Graham-Schonholzer法是在Dobinson法的基础上,再计及换相过程后提出来的。它对交流侧电流的近似处理,是将Dobinson法的用两个正弦波头叠加在120°方波上,改进为叠加在120°+γ的梯形波上,如图3-23所示。梯形波的斜边就是对换相过程的较好近似。
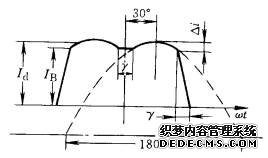
图3-23 Graham-Schonholzer法采用的近似电流波形
为了表达方便,引入换相末电流IB这个量。
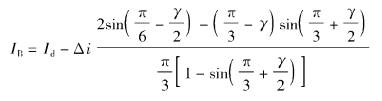 (3-55)
(3-55)IB就是换相结束的时刻流过导通晶闸管的电流值。Δi与前述一样,是电流波头脉动的峰峰值。再引入以IB为分母的电流纹波比rB,即
则图3-23所示的电流波形,即可用IB、rB和换相重叠角γ这三个变量来表示。
对电流波形进行傅里叶分解,可得基波和各次谐波有效值的统一表达式
对电流波形进行傅里叶分解,可得基波和各次谐波有效值的统一表达式
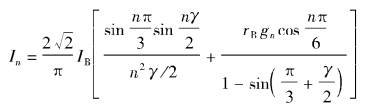 (3-57)
(3-57)式中
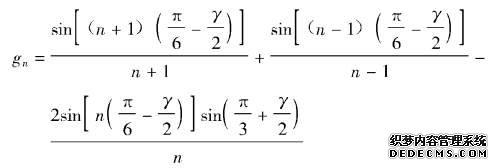
(n=1或n=6k±1,k为正整数) (3-58)
应当注意,当代入n或γ的值出现分母为零的情况时,应利用如下极限公式进行计算:
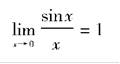
根据计算结果绘出的各次谐波相对于基波的含量曲线如图3-24~图3-29所示。由公式或者曲线中所得的负数值表示有180°相移的情况,应用时取其绝对值即可。电流纹波比rB的确定,根据其定义由式(3-53)和式(3-55)分别计算出Δi和IB即可求得。不过,仔细观察式(3-55)就可以发现,将其等号两边分别除以Δi,即可得到rB与rd这两种电流纹波的关系式。将此关系式绘成图3-30所示的曲线,应用起来非常方便。
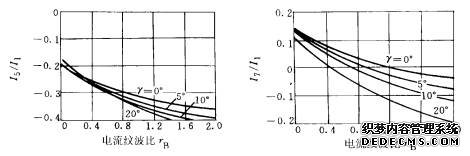
图3-24 Graham-Schonholzer法 图3-25 Graham-Schonholzer法
得到的5次谐波含量曲线 得到的7次谐波含量曲线
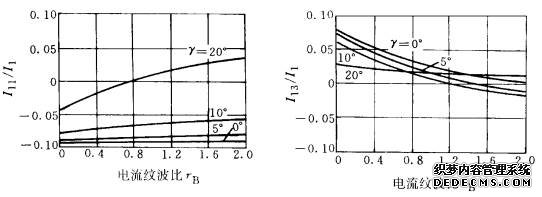
图3-26 Graham-Schonholzer法 图3-27 Graham-Schonholzer法
得到的11次谐波含量曲线 得到的13次谐波含量曲线
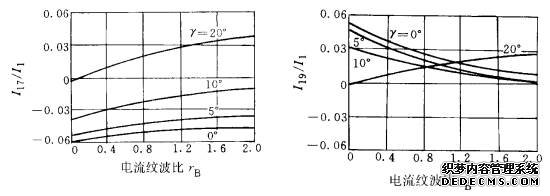
图3-28 Graham-Schonholzer法 图3-29 Graham-Schonholzer法
得到的17次谐波含量曲线 得到的19次谐波含量曲线
主营产品:有源电力滤波器IGBT应用方案,有源滤波器方案定制,apf方案定制,有源滤波器解决方案,apf stack,电力电子积木,感应加热IGBT方案