交流调压电路的通断控制和移相控制方式比较

交流调压电路的通断控制和移相控制方式比较

 

    当1≤n＜M时，电源电流的谐波频率为                 

                                                        
    这对于电源频率ω0=Mω来讲，就是所谓的次谐波（Subhar-monics），也就是小于电源频率的分数次谐波。

    当n=M时，不能直接应用式（3-143）的结果，由傅里叶系数计算的基本公式可得

                                      （3-144）

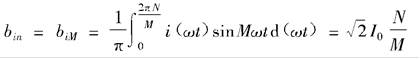                       （3-145）
故

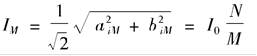             （3-146）
也就是说，电源电流中与电源频率相同的分量与电源电压同相（即位移因数为1），且有效值为晶闸管不关断而全通时有效值的N/M倍。

                                   
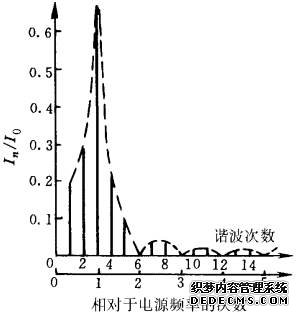
                                 图3-63  通断控制交流调压电路的电流频谱图(M=3,N=2)

                                            (3-147)
则该次谐波分量为零。显然，具有整数倍电源频率的谐波和其他满足式（3-147）的分数倍电源频率谐波为零。例如，在图3-63中，M=3，N=2，因此n=6、9、12等次谐波为零，它们相对于电源频率分别为2次、3次和4次谐波；而对于M=4，N=2的情况，可知n=2、6、8、10等次谐波为零，而对电源频率来讲，它们的次数分别为1/2、3/2、2和5/2次等。

    此外还可以证明，在M和N的某些特定取值下，会出现次谐波电流含量大于电源频率电流含量的情况；而高于电源频率的谐波，其含量总是不会大于电源频率电流的[98]。

    为了更深刻地了解通断控制交流调压电路谐波的情况，还可以与移相控制交流调压电路作一对比。图3-64给出了在相同输出功率下，这两种电路频谱图的对比，可以看到，移相控制电路电流的电源频率成分要大于通断控制时，而其高次谐波成分也远大于通断控制时；通断控制虽然高次谐波少，但在电源频率的附近集中了许多含量很高的分数次谐波。

                          
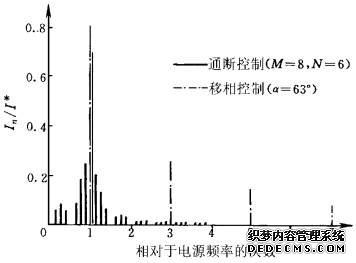
                       图3-64  交流调压电路通断控制方式和移相控制方式电流频谱比较