快捷导航
上海总部：上海市普陀区宁夏路201号绿地科创大厦6楼D座
邮编：200063
总机：021-31358878、52363421
传真：021-31358878-8010
业务邮箱：
guandq@hmelectronics.com.c
n
邮编：200063
总机：021-31358878、52363421
传真：021-31358878-8010
业务邮箱：
guandq@hmelectronics.com.c
n
资讯文章
阻感负载时单相交流调压电路的计算
阻感负载时单相交流调压电路的计算
根据定义，由式（3-91）～式（3-94）还可计算出基波因数、位移因数和功率因数，如图3-45所示。由此图可以看出，这三项指标均随α角的增大而减小。
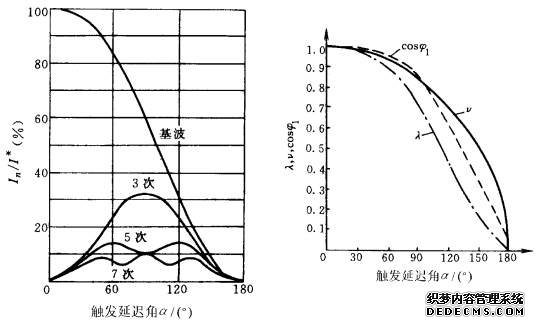
图3-44 电阻负载的单相交流调压 图3-45 电阻负载的单相交流
电路电流基波和谐波的含量 调压电路各项性能指标
阻感负载的单相交流调压电路及其在移相控制方式下的波形如图3-46所示。同样，α为触发延迟角，而电源电压仍如式（3-81）所示。
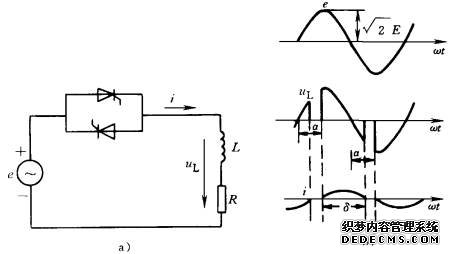
图3-46 阻感负载的单相交流调压电路
a) 电路 b) 波形
由参考文献[97]的分析可知，电路的工作情况由触发延迟角α与负载的功率因数角φL的关系决定。其中
（3-96）在这种情况下，α角的移相范围为φL～180°。
根据电路图，可列出如下电路方程：
根据电路图，可列出如下电路方程：
（3-97）设初始条件为
即可求得电源电流i的表达式
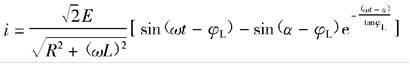（3-98） 设导通角为δ，则有
将上式代入式（3-98）中，得
（3-99）此式给出了α、φL和δ这三个角度之间的关系。当α和φL已知时，即可由此式确定δ角，从而确定式（3-98）所示的电源电流表达式成立的时间区域。为便于查阅，现将α、φL和δ之间的关系绘成曲线如图3-47所示。
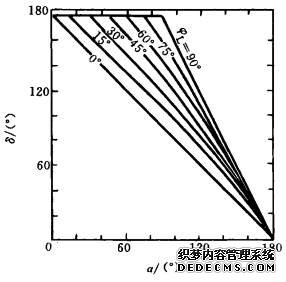
图3-47
根据电源电流表达式，可对其波形进行傅里叶分解，即
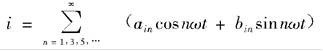（3-100）式中的傅里叶系数分别为
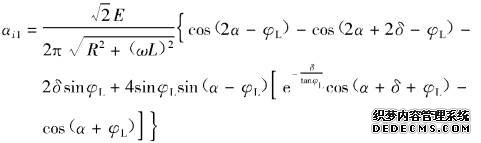（3-101）
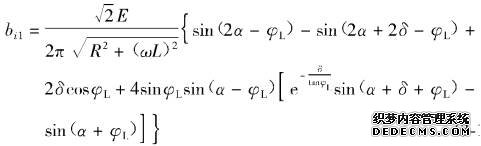（3-102）
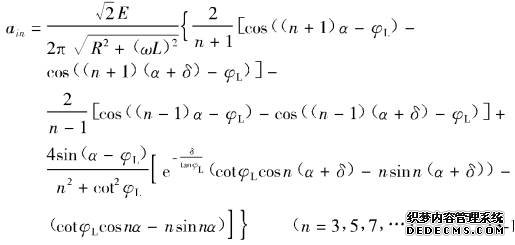（3-103）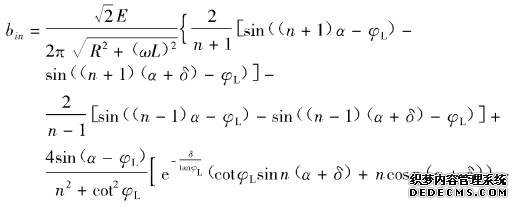
（3-104）于是按下式可得电流基波的有效值和初相角：
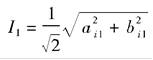（3-105）
（3-106）而各次谐波电流有效值可按下式求得：
（3-107） 另外，电源电流的总有效值也可按下式求出：
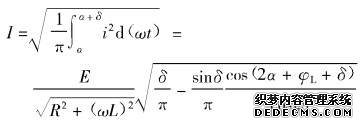（3-108）主营产品：有源电力滤波器IGBT应用方案,有源滤波器方案定制,apf方案定制,有源滤波器解决方案,apf stack,电力电子积木,感应加热IGBT方案